When there is a tangle between two microscopic systems, their properties are associated with each other regardless of the physical distance between the two.
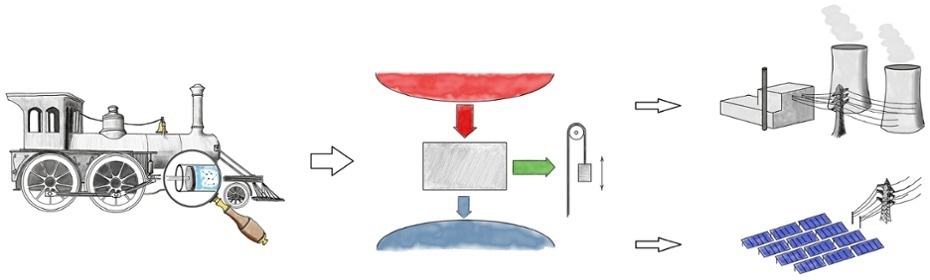
The Carnot cycle is a general model of energy production that can be applied to any thermal energy source. Devised by the pioneering French physicist Sadi Carnot in 1824, when only steam engines were available, it can equally well be applied today to nuclear or solar power plants. Image Credit: University of Amsterdam.
Quantum cryptography, computation, and communication are enabled by manipulating this uniquely quantum phenomenon. While a comparison is made between quantum entanglement and the classical physics of heat, a new study performed has illustrated the limits of this comparison.
The Power of the Second Law
In many cases, the second law of thermodynamics is known to be one of just a few physical laws that are undoubtedly and entirely true. The law defines that the amount of “entropy”, a physical property of any closed system, can never be reduced.
It adds an “arrow of time” to daily incidents, identifying which processes could be reversed and which could not be. It describes why an ice cube positioned on a hot stove will melt, and why compressed gas will always fly out of its container (and can never be put in) when a valve is opened to the atmosphere.
It is possible for only states of equal energy and entropy to be reversibly transformed from one to the other. This reversibility condition resulted in the breakthrough of thermodynamic processes like the (idealized) Carnot cycle.
This discovery shows an upper limit to how effectively one can transform heat into energy, or vice versa, by cycling a closed system via various pressures and temperatures.
Quantum Entropy
The beauty of the second law of thermodynamics is its applicability to any macroscopic system—irrespective of the microscopic details. In quantum systems, one of these details is known as entanglement: a quantum connection that makes isolated components of the system share properties.
Interestingly, several similarities have been identified between thermodynamics and quantum entanglement, although quantum systems are primarily studied at the microscopic level. Researchers have revealed a notion of “entanglement entropy” that mimics thermodynamical entropy, at least for idealized quantum systems that are ideally separated from their environment.
Quantum entanglement is a key resource that underlies much of the power of future quantum computers. To make effective use of it, we need to learn how to manipulate it.
Ludovico Lami, Quantum Information Researcher, University of Amsterdam
A basic question became whether entanglement could always be manipulated in a reversible manner, in direct analogy to the Carnot cycle. Vitally, this reversibility would need to hold, at least in theory, even for noisy (“mixed”) quantum systems that are not perfectly separated from their surroundings.
It was presumed that a “second law of entanglement” could be fixed, embodied in a single function that would help generalize the entanglement entropy and control all entanglement manipulation protocols. This conjecture is featured in a renowned list of unsolved problems in quantum information theory.
No Second Law of Entanglement
Solving this long-standing open question, a study performed by Lami (earlier at the University of Ulm and presently at QuSoft and the University of Amsterdam) and Bartosz Regula (University of Tokyo) illustrates that manipulation of entanglement is basically irreversible, putting aside any hopes of fixing a second law of entanglement.
This new outcome depends on the construction of a specific quantum state which is highly expensive to create utilizing pure entanglement. Making this state will always lead to a loss of a few of these entanglements, as it is not possible to completely recover the invested entanglement. Consequently, it is naturally impossible to shift this state into another and further back again.
Since the method utilized here fails to assume what actual transformation protocols are utilized, it bars the reversibility of entanglement in all feasible settings. It employs all protocols, presuming they do not produce new entanglement themselves.
Using entangling operations would be like running a distillery in which alcohol from elsewhere is secretly added to the beverage.
Ludovico Lami, Quantum Information Researcher, University of Amsterdam
Lami added, “We can conclude that no single quantity, such as the entanglement entropy, can tell us everything there is to know about the allowed transformations of entangled physical systems. The theory of entanglement and thermodynamics are thus governed by fundamentally different and incompatible sets of laws.”
This might imply that explaining quantum entanglement is not as easy as believed by the researchers. But instead of being a disadvantage, the immensely greater complexity of the theory of entanglement makes a comparison to the classical laws of thermodynamics that might enable one to make use of the entanglement to reach feats that would be completely inconceivable otherwise.
For now, what we know for certain is that entanglement hides an even richer and more complicated structure that we had given it credit for.
Ludovico Lami, Quantum Information Researcher, University of Amsterdam
Journal Reference:
Lami, L & Regula, B (2023) No second law of entanglement manipulation after all. Nature Physics. doi.org/10.1038/s41567-022-01873-9.