Sep 20 2019
Structures called “time crystals,” which repeat in time similar to traditional crystals that repeat in space, have recently gained the attention and imagination of scientists from several disciplines.
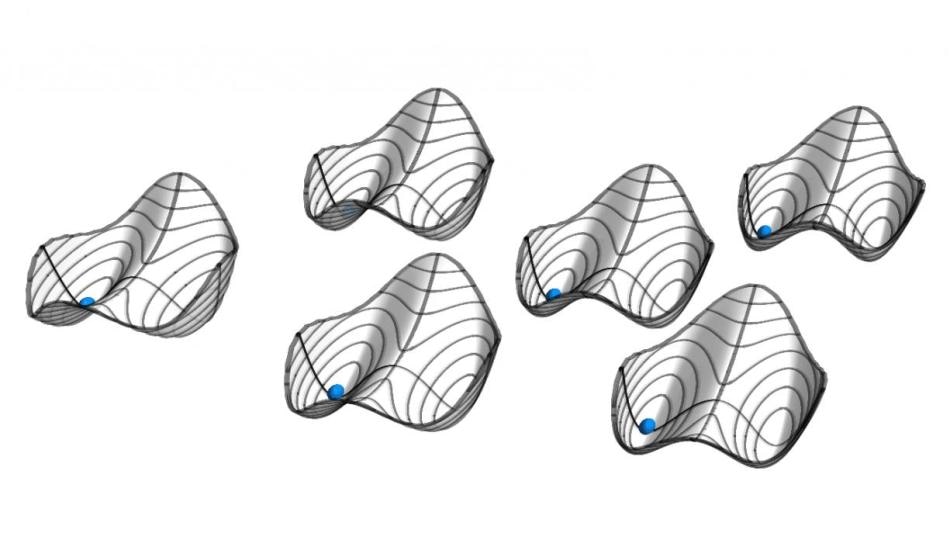 Quasi potentials of six parametric oscillators with weak all-to-all coupling. Stable solutions are located at the minima. The balls indicate the symmetric solution, where all oscillators are in phase. The Hamiltonian H governing the motion of the system has period T, while the solution itself has period 2T. This discrete time translation symmetry breaking makes the system a discrete time crystal. (Image credit: ETH Zurich/D-PHYS Toni Heugel)
Quasi potentials of six parametric oscillators with weak all-to-all coupling. Stable solutions are located at the minima. The balls indicate the symmetric solution, where all oscillators are in phase. The Hamiltonian H governing the motion of the system has period T, while the solution itself has period 2T. This discrete time translation symmetry breaking makes the system a discrete time crystal. (Image credit: ETH Zurich/D-PHYS Toni Heugel)
Although the idea has emerged from the framework of quantum many-body systems, at present, ETH physicists have created an all-around system that explains links to classical studies dating back almost two centuries, thereby offering a consolidative platform to analyze apparently distinct phenomena.
Atoms in a crystal are highly ordered and occupy definite locations forming spatial patterns. Seven years ago, Frank Wilczek, the 2004 Physics Nobel laureate, speculated the possibility of a “time analogue of crystalline spatial order”—systems exhibiting sustained periodic temporal modulations in their lowest energy state. The idea of such structures that have an oscillating ground state is extremely fascinating.
Unfortunately, very soon after the concept was reported, it was demonstrated that such time crystals are not feasible without breaking fundamental laws of physics. However, not all was lost. Subsequent theory work indicated that periodical driving of quantum many-body systems leads to the emergence of new persistent time correlations that are evocative of Wilczek’s time crystals.
These driven systems were named “discrete time crystals.” In 2017, the first experimental achievements of such states were announced in ensembles of coupled particles (electrons, ions, and nuclei) that exhibit quantum-mechanical properties.
A Not-So-Brief History of Time Crystals
Soon, intelligent observers found out unique similarities between discrete time crystals in quantum systems and what are called parametric resonators, a classical physics concept dating back to study by Michael Faraday in 1831. However, the link between these two studies remained obscure. Currently, a new framework has made a long way in eliminating the uncertainties regarding the similarities between periodically driven classical and quantum systems.
Reporting in an article published in the Physical Review Letters journal on September 19th, 2019, ETH PhD student Toni Heugel and Master student Matthias Oscity, collaborating with Dr Ramasubramanian Chitra and Prof Oded Zilberberg from the Institute for Theoretical Physics and with Dr Alexander Eichler from the Laboratory for Solid State Physics, describe a theoretical and experimental study that determines the way discrete time crystals can be produced that, on the one hand, need no quantum mechanical effects and, on the other hand, exhibit real many-body effects—a property of discrete time crystals reported in quantum systems.
Many Ways to Subharmonic Frequencies
There is one evident analogy between classical parametric resonators and experimentally achieved discrete time crystals in quantum many-body systems—both exhibit emergent dynamics at frequencies that are fractions of the drive frequency.
When it comes to discrete time crystals, the occurrence of oscillations at such subharmonic frequencies interrupts the driven system’s temporal periodicity, thus offering a form of “time analogue” to crystalline spatial order, in which the symmetry of space is destroyed.
In the context of classical parametrically driven systems, subharmonic frequencies emerge in more regular ways: For example, a child on a swing alters the centre of gravity at twice the frequency of the ensuing oscillation; or a runner’s ponytail oscillates at half the frequency of the vertical head movement.
However, are these distinct phenomena related to one another in any way? According to the ETH physicists, they are indeed related. Specifically, they indicate where many-body features arise in classical systems. They achieved this by considering classical nonlinear oscillators that are tunably coupled to one another.
Unifying Framework for Periodically Driven Classical and Quantum Systems
The fact that parametric oscillators turn unstable for specific driving frequencies and strengths and subsequently undergo what is called a period-doubling bifurcation is largely known. Beyond the bifurcation, they oscillate at half their driving frequency. Heugel, Oscity, and their coworkers investigate what happens as numerous such oscillators are coupled together.
In calculations and even in experiments—performed with two strings that are variably coupled to one another—they find two dissimilar regimes. In the case of strong coupling, the two-string system travels collectively, typically reconstructing the movements of the ponytail of a runner or the child on a swing.
But if the coupling between the strings is weak, each string’s dynamics is close to that exhibited by the uncoupled system. As a result, rather than bifurcating collectively, the coupled oscillators bifurcate individually at somewhat different parameters of the drive. This results in richer overall dynamics, which becomes more complex than ever as the systems turn larger.
The ETH scientists assert that weakly coupled modes such as these are analogous to the ones that arise in quantum many-body systems. This suggests that their framework might offer an explanation to the behaviours observed experimentally in these systems. Furthermore, the new study proposes general conditions for producing classical many-body time crystals.
These could eventually be used to interpret as well as investigate features of their quantum counterparts. Collectively, these outcomes offer a robust consolidative framework for periodically driven quantum and classical systems that exhibit dynamics at emergent subharmonic frequencies. These systems have so far been characterized in completely different contexts, but might be not so distinct after all.