May 30 2019
It is extremely challenging to accurately calculate the dynamics of a number of interacting quantum particles accurately.
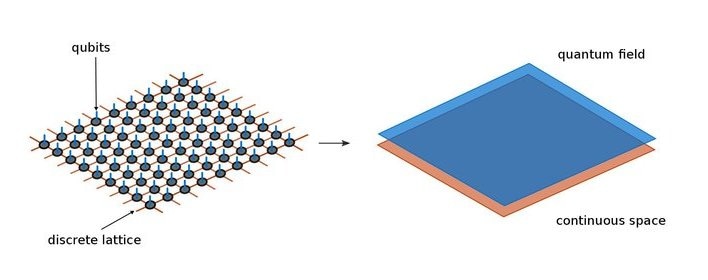Standard tensor network states describe quantum systems that live on a discrete space, or lattice, for example an array of qubits. Continuous tensor networks, on the other hand, shrink the lattice distances until they are infinitely small and thus restore the continuity of space. This way, they can deal with quantum fields more directly. (Image credit: Max Planck Institute of Quantum Optics)
However, for such kinds of systems, a potential calculation technique called tensor networks is available. The theory division at the Max Planck Institute of Quantum Optics is now studying these networks. The original focus of the tensor network was on quantum particles that are generally limited to a lattice, just as they form in crystals for instance, or in the quantum registers of upcoming quantum computers.
In a recent study, the theory division director Ignacio Cirac and the postdoctoral researcher Antoine Tilloy were able to extend this method to the continuum. The ultimate goal is to develop a sophisticated calculation technique for the quantum field theories that explain the physics’ fundamental forces.
One of the important challenges of physics is elucidating the systems in which several quantum particles interact and together create novel phenomena. Superconductivity is one example of such a quantum many-body phenomenon. The current challenge is the effect of particles on one another. Consequently, the quantum mechanical equations describing this overall behavior can be obtained, but cannot solved accurately.
In quantum mechanics to be specific, the dynamical equation should be able to capture all the potential states the system possibly can be in, and there can be several. Quantum bits (qubits) are one example that is presently popular in physics and are achieved, for example, from electrically charged atoms or exclusively prepared electrons. Qubits like these have two opposing states, which can assume the values of one and zero. However, the qubit can also be placed in any superposition of those two opposing states, unlike a “classical” bit. If two qubits are combined with what is known as a quantum gate, the abstract mathematical space of all conceivable quantum states increases by twofold. Moreover, each extra qubit doubles it again. This exponentially increasing number of potential quantum states literally overruns the data memories and processors in traditional computers. After over a few dozen qubits, even supercomputers will fail. Only quantum computers, which follow the rules of quantum mechanics themselves, will be able to handle the dynamics of bigger quantum systems.
Making the incalculable calculable
Since Ignacio Cirac and his team are among the pioneers of this evolving area of quantum information technology, the example of the qubits fits suitably. The “tensor networks,” technique, which is the topic of this study, also comes from this research field. It helps in ingeniously decreasing the massive space of all potential quantum states of a multi-particle system to a size that can be calculated accurately.
“Imagine all possible quantum states of a many-particle system as a huge circular area,” explained Antoine Tilloy. “But the states that are really relevant for our system fit within a much smaller circle.” Now the art lies in detecting this tiny circle in an abstract mathematical space, and that is what tensor networks can actually do.
As a postdoctoral researcher in Cirac’s team, Tilloy has jointly published an article on tensor networks in the journal, Physical Review X. Initially, the physicists applied the tensor networks to arrays of separate qubits. Thus, these networks were originally depending on a network of abstract mathematical objects—somewhat like a mathematical series of pearls, living on distinct positions.
Furthermore, tensor networks demonstrated to be an effective tool to perform calculations for a bulk class of quantum system limited to grids. This achievement eventually gave an idea to theoretical research teams across the world—is it possible to apply this technique to physical systems that do not live on grids, but instead in continuum space? In brief, the answer is yes. As a matter of fact, the technique of tensor networks can also be extended to the continuum and this is what Cirac and Tilloy showed in their recent study.
New tool for quantum field theories
For this novel toolbox, the so-called quantum field theories can prove to be a major area of application. Such theories lay the groundwork for current physical worldview. They precisely show how three of the four fundamental forces of physics work in accordance with quantum mechanics. Virtual particles mediate these forces, and these particles exist only for a brief period of time required to convey their force. For instance, in the electric force, virtual light quanta are the mediating particles.
This falls under what is known as quantum electrodynamics and is well understood. Things get more complicated with what is known as quantum chromodynamics.
Antoine Tilloy, Postdoctoral Researcher, Max Planck Institute of Quantum Optics
Quantum chromodynamics, or QCD for short, elucidates the forces existing between the quarks, which sequentially create the building blocks of the atomic nuclei, the neutrons and protons. The strongest force in physics is mediated by “adhesive particles,” or gluons, and this “glues” the quarks together.
However, the gluons are different from the virtual photons and can also have a powerful effect on one another. This “self-interaction” results in the unnecessary fact that QCD equations can only be resolved in borderline cases, at extremely high energy. With regards to lower energies—the unusual state of matter in the environment—this cannot be realized. Due to this reason, physicists have to work with approximate solutions to date. Here, the usual step is to break the continuum down into a synthetic grid of points for which a robust computer can subsequently compute approximate solutions.
“This step of discretization is complex,” stated Tilloy.
Moreover, these simplifications invariably have the drawback of breaking an important symmetry of nature when splitting the continuum into an artificial grid of distinct points. Therefore, they are made to move away from the actual physics. Here, the technique of continuous tensor networks can possibly provide help because it eliminates the need for this prior discretization of space. Maybe gluons’ and quarks’ behavior at low energies will be understood someday. Currently, it is still a major concern, but the newly discovered continuous tensor networks could already be a part of the solution.