Apr 12 2013
Quantum computers promise to perform certain types of operations much more quickly than conventional digital computers. But many challenges must be addressed before these ultra-fast machines become available, among them, the loss of order in the systems – a problem known as quantum decoherence – which worsens as the number of bits in a quantum computer increases.
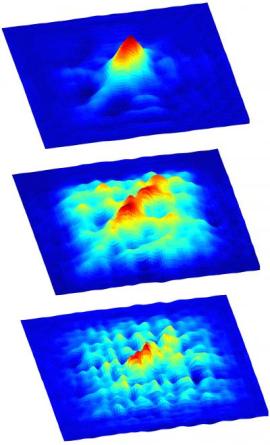These images show that quantum correlations in the Georgia Tech Bose-Einstein condensate are highly concentrated at first (top graph), then slowly diffuse outward (lower two graphs). The peaks show the localization of the correlations. Credit: Image courtesy of Chandra Raman
One proposed solution is to divide the computing among multiple small quantum computers that would work together much as today's multi-core supercomputers team up to tackle big digital operations. The individual computers in such a system could communicate quantum information using Bose-Einstein condensates (BECs) – clouds of ultra-cold atoms that all exist in exactly the same quantum state. The approach could address the decoherence problem by reducing the number of bits necessary for a single computer.
Now, a team of physicists at the Georgia Institute of Technology has examined how this Bose-Einstein communication might work. The researchers determined the amount of time needed for quantum information to propagate across their BEC, essentially establishing the top speed at which such quantum computers could communicate.
"What we did in this study was look at how this kind of quantum information would propagate," said Chandra Raman, an associate professor in Georgia Tech's School of Physics. "We are interested in the dynamics of this quantum information flow not just for quantum information systems, but also more generally for fundamental problems in physics."
The research is scheduled to be published in the April 19 online edition of the journal Physical Review Letters. The research was funded by the U.S. Department of Energy (DOE) and the National Science Foundation (NSF). The work involved both an experimental physics group headed by Raman and a theoretical physics group headed by associate professor Carlos Sa De Melo, also in the Georgia Tech School of Physics.
The researchers first assembled a gaseous Bose-Einstein condensate that consisted of as many as three million sodium atoms cooled to nearly absolute zero. To begin the experiment, they switched on a magnetic field applied to the BEC that instantly placed the system out of equilibrium. That triggered spin-exchange collisions as the atoms attempted to transition from one ground state to a new one. Atoms near one another became entangled, pairing up with one atom's spin pointing up, and the other's pointing down. This pairing of opposite spins created a correlation between pairs of atoms that moved through the entire BEC as it established a new equilibrium.
The researchers, who included graduate student Anshuman Vinit and former postdoctoral fellow Eva Bookjans, measured the correlations as they spread through the cloud of cold atoms. At first, the quantum entanglement was concentrated in space, but over time, it spread outward like drop of dye diffuses through water.
"You can imagine having a drop of dye that is concentrated at one point in space," Raman said. "Through diffusion, the dye molecules move throughout the water, slowly spreading throughout the entire system."
The research could help scientists anticipate the operating speed for a quantum computing system composed of many cores communicating through a BEC.
"This propagation takes place on the time scale of ten to a hundred milliseconds," Raman said. "This is the speed at which quantum information naturally flows through this kind of system. If you were to use this medium for quantum communication, that would be its natural time scale, and that would set the timing for other processes."
Though relevant to communication of quantum information, the process also showed how a large system undergoing a phase transition does so in localized patches that expand to attempt to incorporate the entire system.
"An extended system doesn't move from one phase to another in a uniform way," said Raman. "It does this locally. Things happen locally that are not connected to one another initially, so you see this inhomogeneity."
Beyond quantum computing, the results may also have implications for quantum sensing – and for the study of other physical systems that undergo phase transitions.
"Phase transitions have universal properties," Raman noted. "You can take the phase transitions that happen in a variety of systems and find that they are described by the same physics. It is a unifying principle."
Raman hopes the work will lead to new ways of thinking about quantum computing, regardless of its immediate practical use.
"One paradigm of quantum computing is to build a linear chain of as many trapped ions as possible and to simultaneously engineer away as many challenges as possible," he said. "But perhaps what may be successful is to build these smaller quantum systems that can communicate with one another. It's important to try as many things as possible and to keep an open mind. We need to try to understand these systems as well as we can."