Dec 17 2018
Quantum computing and quantum information processing technology have gained interest in fields that have emerged recently. Among various significant and basic issues in present-day science, solving the Schroedinger Equation (SE) of atoms and molecules is one of the main goals in physics, chemistry, and their related fields.
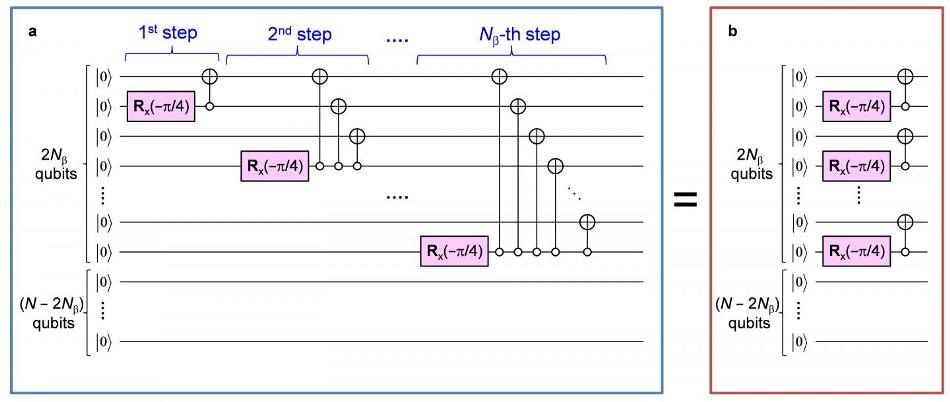(a) (Left) Previously proposed quantum circuit. (b) (Right) New parallelized quantum circuit. In (b), the complexity of the circuit is reduced drastically. (Image credit: K. Sugisaki, T. Takui et al./Osaka City University)
SE is the “First Principle” of non-relativistic quantum mechanics, the solutions of which called as wave functions can offer any information related to electrons within atoms and molecules, estimating their physicochemical properties and chemical reactions. Scientists from Osaka City University (OCU) in Japan, Dr K. Sugisaki, Prof. K. Sato, and Prof. T. Takui and colleagues have discovered a quantum algorithm that allows full configuration interaction (Full-CI) calculations to be carried out for any open shell molecules without exponential/combinatorial explosion.
Full-CI offers SE’s exact numerical solutions, which are one of the unmanageable challenges with respect to any supercomputer. The execution of such a quantum algorithm enables the speeding up of the implementation of practical quantum computers. The study has been published in the first issue of the Open Access Journal Chemical Physics Letters X on December 13th, 2018.
According to the OCU research group, “As Dirac claimed in 1929 when quantum mechanics was established, the exact application of mathematical theories to solve SE leads to equations too complicated to be soluble [1]. In fact, the number of variables to be determined in the Full-CI method grows exponentially against the system size, and it easily runs into astronomical figures such as exponential explosion. For example, the dimension of the Full-CI calculation for benzene molecule C6H6, in which only 42 electrons are involved, amounts to 1044, which are impossible to be dealt with any supercomputers.”
The OCU research group noted that the age of the quantum computers could be dated back to a suggestion by Feynman in 1982 that it is possible to simulate quantum mechanics using a computer itself developed with quantum mechanical elements that abide by quantum mechanical laws. Nearly two decades later, Prof. Aspuru-Guzik from Harvard University (Toronto University since 2018) and colleagues put forward a quantum algorithm with the ability to calculate the energies of atoms and molecules not exponentially rather polynomially against the number of the variables of the systems, accomplishing a path-breaking achievement in the field of quantum computers on quantum chemistry [2].
Optimal approximate wave-functions close to the exact wave-functions of SE under investigation are needed to apply Aspuru’s quantum algorithm to the Full-CI calculations on quantum computers; otherwise, bad wave-functions require an extreme number of repeated calculations steps to attain the exact ones, inhibiting the benefits of quantum computing.
This challenge turns out to be extremely critical for any open shell systems, which include a number of unpaired electrons that do not take part in chemical bonding. The OCU scientists have overcome this difficulty, one of the most unmanageable problems in quantum science, and made a path-breaking achievement in executing a quantum algorithm, producing specific wave-functions called configuration state functions in polynomial computing time in 2016 [3].
The algorithm proposed earlier needs a substantial number of quantum circuit gate operations proportional to the squares of the number N, which signifies the number of down-spins of the unpaired electrons in the system. As a result, if there is an increase in N, the total computing time does not increase exponentially but drastically. Furthermore, it is necessary for the quantum circuits’ complexity to be reduced to enable practical usage of the algorithm and quantum programming architecture.
A new quantum algorithm makes use of the germinal spin functions, known as Serber construction, and decreases the number of the gate operations to merely 2N, implementing parallelism of the quantum gates. According to the OCU group, “This is the first example of practical quantum algorithms, which make quantum chemical calculations realizable on quantum computers equipped with a sizable number of qubits. These implementations empower practical applications of quantum chemical calculations on quantum computers in many important fields.”
[1] P.A.M. Dirac, Quantum mechanics of many-electron systems. Proc. R. Soc. London, Ser. A 1929, 123, 714-733.
[2] A. Aspuru-Guzik, A. D. Dutoi, P. J. Love, M. Head-Gordon, Science 2005, 309, 1704.
[3] K. Sugisaki, S. Yamamoto, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi, T. Takui, J. Phys. Chem. A 2016, 120, 6459-6466. DOI: 10.1021/acs.jpca.6b04932