Feb 24 2015
Advances in experimental and theoretical physics enable a deeper understanding of the dynamics and properties of quantum many-body systems.
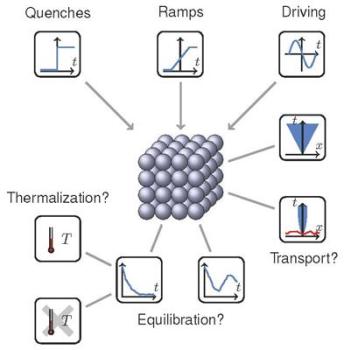 Illustration of the various options to influence the properties of quantum many-body systems. (Theory Division, MPQ)
Illustration of the various options to influence the properties of quantum many-body systems. (Theory Division, MPQ)
Considering that one cubic centimetre of matter already contains about 1019 to 1023 particles it is hard to imagine that physicists nowadays can prepare ensembles comprising only some hundred, or even just a handful of atoms. What is more, they have improved their techniques to the extent that they can manipulate such particles individually or jointly and can fine tune their interactions. Driven by on new numerical techniques, powerful supercomputers, and new mathematical techniques the theoretical description of such systems has seen equally impressive progress. In a recent review article in Nature Physics (3rd of February 2015) the team of Prof. Dr. Jens Eisert, Mathis Friesdorf (both from the Dahlem Center for Complex Quantum Systems, Freie Universität Berlin) and Dr. Christian Gogolin, postdoctoral researcher in the Theory Division of Prof. Ignacio Cirac at MPQ (Garching) and research fellow at ICFO (Barcelona), discuss the various quantum systems that have been realised and how they are described theoretically, and give an outlook on promising developments.
Particularly important in the quest for a better understanding of quantum many-body systems are the processes that take place while a system is on its way back to equilibrium after being perturbed externally. Here the challenge is to bridge the gap between the microscopic description of the local dynamics and the well-known macroscopic description in terms of statistical ensembles. Which picture applies depends crucially on the size of the system and the kind of interaction between the particles.
In many experiments systems with short range interactions are realised. Particularly fruitful have been techniques based on ultracold atomic gases in so-called optical lattices – essentially grids of standing waves generated by counterpropagating laser beams. Such systems can for example be used as models for ferromagnetic materials.
A very interesting aspect of condensed matter physics which can also be investigated with such systems is transport – for example that of electrons and thereby electric charges in crystals. In close collaboration experimentalists and theorists thereby find out which parameters determine properties such as the conductivity, and how defects and disorder influence the mobility of particles.
Large quantum many-body systems are often tackled with statistical methods from thermodynamics. Of particular interest is here the temporal evolution when global parameters – such as temperature or an external field – are changed. Such a change can be sudden or can occur more slowly over extended amounts of time, or even happen periodically. The scientists thereby investigate whether, how, and on what time scales systems go to a new equilibrium state. In many systems "critical" values for the parameters exist at which a sudden transition to a new "phase" with drastically different properties can be observed – analogous to the melting of ice above zero degree Celsius. Understanding the dynamics of such phase transitions is an ongoing challenge for theoreticians.
Such quantum many-body systems have also proven useful as simulators of large and possibly multi-dimensional lattice systems whose non-equilibrium dynamics is not accessible with analytical or numerical tools. Experimental realisations of such systems can thus be regarded as analogue simulators with which these restrictions can be overcome.
Despite the tremendous progress many questions are still open. Some of the riddles of the tendency to evolve back into equilibrium are now understood, but the question of what defines the time scales on which these relaxation processes happen is still pretty much open. Moreover in the future scientists want to investigate not only closed systems, but also those in which interactions with the environment causes decoherence and dissipation. Such, usually harmful and unwanted processes – if carefully engineered – can be used to prepare interesting phases of matter.