Nov 18 2014
Researchers try to meet the inexorable demands made on the telecommunications grid by improving various components. In October 2014, for instance, scientists at the Eindhoven University of Technology in The Netherlands did their part by setting a new record for transmission down a single optical fiber: 255 terabits per second.
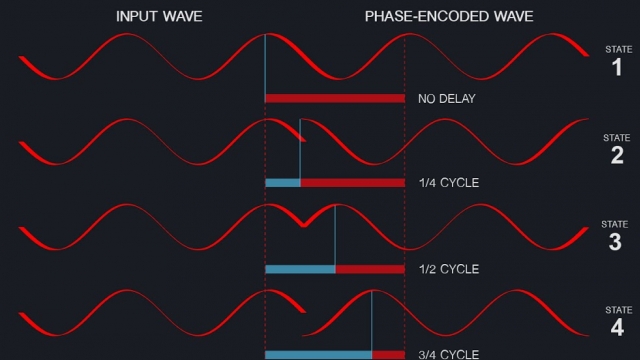Figure 1: By passing it through a special crystal, a light wave’s phase---denoting position along the wave’s cycle---can be delayed. A delay of a certain amount can denote a piece of data. In this experiment light pulses can be delayed by a zero amount, or by ¼ of a cycle, or 2/4, or ¾ of a cycle. Thus a light pulse can be in one of four states. Credit: Kelley/JQI
Alan Migdall and Elohim Becerra and their colleagues at the Joint Quantum Institute do their part by attending to the accuracy at the receiving end of the transmission process. They have devised a detection scheme with an error rate 25 times lower than the fundamental limit of the best conventional detector. They did this by employing not passive detection of incoming light pulses. Instead the light is split up and measured numerous times.
The new detector scheme is described in a paper published in the journal Nature Photonics.
“By greatly reducing the error rate for light signals we can lessen the amount of power needed to send signals reliably,” says Migdall. “This will be important for a lot practical applications in information technology, such as using less power in sending information to remote stations. Alternatively, for the same amount of power, the signals can be sent over longer distances.”
Phase Coding
Most information comes to us nowadays in the form of light, whether radio waves sent through the air or infrared waves send up a fiber. The information can be coded in several ways. Amplitude modulation (AM) maps analog information onto a carrier wave by momentarily changing its amplitude. Frequency modulation (FM) maps information by changing the instantaneous frequency of the wave. On-off modulation is even simpler: quickly turn the wave off (0) and on (1) to convey a desired pattern of binary bits.
Because the carrier wave is coherent---for laser light this means a predictable set of crests and troughs along the wave---a more sophisticated form of encoding data can be used. In phase modulation (PM) data is encoded in the momentary change of the wave’s phase; that is, the wave can be delayed by a fraction of its cycle time to denote particular data. How are light waves delayed? Usually by sending the waves through special electrically controlled crystals.
Instead of using just the two states (0 and 1) of binary logic, Migdall’s experiment waves are modulated to provide four states (1, 2, 3, 4), which correspond respectively to the wave being un-delayed, delayed by one-fourth of a cycle, two-fourths of a cycle, and three-fourths of a cycle. The four phase-modulated states are more usefully depicted as four positions around a circle (figure 2). The radius of each position corresponds to the amplitude of the wave, or equivalently the number of photons in the pulse of waves at that moment. The angle around the graph corresponds to the signal’s phase delay.
The imperfect reliability of any data encoding scheme reflects the fact that signals might be degraded or the detectors poor at their job. If you send a pulse in the 3 state, for example, is it detected as a 3 state or something else? Figure 2, besides showing the relation of the 4 possible data states, depicts uncertainty inherent in the measurement as a fuzzy cloud. A narrow cloud suggests less uncertainty; a wide cloud more uncertainty. False readings arise from the overlap of these uncertainty clouds. If, say, the clouds for states 2 and 3 overlap a lot, then errors will be rife.
In general the accuracy will go up if n, the mean number of photons (comparable to the intensity of the light pulse) goes up. This principle is illustrated by the figure to the right, where now the clouds are farther apart than in the left panel. This means there is less chance of mistaken readings. More intense beams require more power, but this mitigates the chance of overlapping blobs.
Twenty Questions
So much for the sending of information pulses. How about detecting and accurately reading that information? Here the JQI detection approach resembles “20 questions,” the game in which a person identifies an object or person by asking question after question, thus eliminating all things the object is not.
In the scheme developed by Becerra (who is now at University of New Mexico), the arriving information is split by a special mirror that typically sends part of the waves in the pulse into detector 1. There the waves are combined with a reference pulse. If the reference pulse phase is adjusted so that the two wave trains interfere destructively (that is, they cancel each other out exactly), the detector will register a nothing. This answers the question “what state was that incoming light pulse in?” When the detector registers nothing, then the phase of the reference light provides that answer, … probably.
That last caveat is added because it could also be the case that the detector (whose efficiency is less than 100%) would not fire even with incoming light present. Conversely, perfect destructive interference might have occurred, and yet the detector still fires---an eventuality called a “dark count.” Still another possible glitch: because of optics imperfections even with a correct reference–phase setting, the destructive interference might be incomplete, allowing some light to hit the detector.
The way the scheme handles these real world problems is that the system tests a portion of the incoming pulse and uses the result to determine the highest probability of what the incoming state must have been. Using that new knowledge the system adjusts the phase of the reference light to make for better destructive interference and measures again. A new best guess is obtained and another measurement is made.
As the process of comparing portions of the incoming information pulse with the reference pulse is repeated, the estimation of the incoming signal’s true state was gets better and better. In other words, the probability of being wrong decreases.
Encoding millions of pulses with known information values and then comparing to the measured values, the scientists can measure the actual error rates. Moreover, the error rates can be determined as the input laser is adjusted so that the information pulse comprises a larger or smaller number of photons. (Because of the uncertainties intrinsic to quantum processes, one never knows precisely how many photons are present, so the researchers must settle for knowing the mean number.)
A plot of the error rates shows that for a range of photon numbers, the error rates fall below the conventional limit, agreeing with results from Migdall’s experiment from two years ago. But now the error curve falls even more below the limit and does so for a wider range of photon numbers than in the earlier experiment. The difference with the present experiment is that the detectors are now able to resolve how many photons (particles of light) are present for each detection. This allows the error rates to improve greatly.
For example, at a photon number of 4, the expected error rate of this scheme (how often does one get a false reading) is about 5%. By comparison, with a more intense pulse, with a mean photon number of 20, the error rate drops to less than a part in a million.
The earlier experiment achieved error rates 4 times better than the “standard quantum limit,” a level of accuracy expected using a standard passive detection scheme. The new experiment, using the same detectors as in the original experiment but in a way that could extract some photon-number-resolved information from the measurement, reaches error rates 25 times below the standard quantum limit.
“The detectors we used were good but not all that heroic,” says Migdall. “With more sophistication the detectors can probably arrive at even better accuracy.”
The JQI detection scheme is an example of what would be called a “quantum receiver.” Your radio receiver at home also detects and interprets waves, but it doesn’t merit the adjective quantum. The difference here is single photon detection and an adaptive measurement strategy is used. A stable reference pulse is required. In the current implementation that reference pulse has to accompany the signal from transmitter to detector.
Suppose you were sending a signal across the ocean in the optical fibers under the Atlantic. Would a reference pulse have to be sent along that whole way? “Someday atomic clocks might be good enough,” says Migdall, “that we could coordinate timing so that the clock at the far end can be read out for reference rather than transmitting a reference along with the signal.”