Sep 27 2013
Simulating solid state properties with precisely controlled quantum systems is an important goal of the Quantum Many-Body Systems Division at MPQ. Now the team around Professor Immanuel Bloch (Chair for Experimental Physics at the Ludwig-Maximilians-Universität Munich and Director at MPQ) has come again a step closer to it – to be precise, to the understanding of processes in ferromagnetic solid state crystals in which elementary excitations, so-called magnons, can emerge.
About 80 years ago the German physicist Hans Bethe deduced from a theoretical model that in one-dimensional ferromagnets two of those elementary magnetic excitations can form a bound state. Like two tiny bar magnets, two atoms can stick together and form a new particle that propagates in the crystal. The MPQ team has now succeeded to observe these most elementary mobile magnetic domains, the two-magnon states, directly and to resolve their dynamics with time-resolved measurements (Nature, AOP 25 September 2013). This study complements conventional spectroscopy in solid state crystals which yields information on momentum and frequency of the magnetic excitations. Bound states of excitations can influence the thermal conductance properties of low-dimensional ferromagnets or the propagation speed of quantum information in magnetic wires.
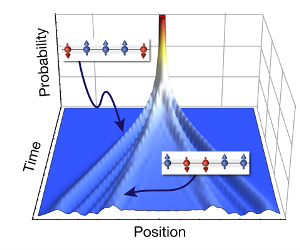Illustration of how the magnons (red) are allowed to propagate in a chain of regularly aligned atoms (blue). Upper left: free magnons move in an anti-correlated fashion. Lower right: the two spins of the compound state stay together throughout their walk. Graphic: MPQ, Quantum Many-Body Systems Division
The magnetic properties of certain materials have been known for centuries, and they have been used for a variety of applications almost quite as long. Today, this behaviour is very well understood at the microscopic level: magnetism goes back to the angular momentum – the spin – of the electrons in the outer shell of the atoms that build up a solid state crystal. In ferromagnetic matter these spins are aligned within the so-called “Weiss” domains.
Similar conditions can be prepared in quantum crystals if the atoms have a defined spin. To this end a cloud of extremely cold (i.e. extremely slow) rubidium atoms is loaded into an optical lattice, generated by crosswise superposition of standing laser waves. The periodically arranged bright patches of the lattice are the sites on which the atoms are allowed to settle down. The dark areas act as barriers, the height of which is determined by the intensity of the laser light. As long as the lattice is comparably shallow, the atoms are able to “tunnel” through the barrier to their neighbouring site. In the experiment described here, the scientists restrict their motion to one direction. As a result the atoms are arranged in ten decoupled one-dimensional “tubes” of more or less the same length.
In the beginning the laser intensity is rather high, and the quantum crystal forms a so-called “Mott-insulator”: each lattice site is occupied with exactly one atom, fixed in space. The atoms are thereby lined up like pearls on a chain with all spins pointing in the same direction – in other words the chain represents a perfect ferromagnetic quantum magnet. A couple of months ago, in a similar experimental set-up, the Bloch group were able to change the spin-direction of one individual atom and to track the propagation of the resulting spin wave throughout the quantum magnet.
Now they went one step further: by precise addressing and application of microwave pulses they flipped the spins of two neighbouring atoms in the centre of each fully magnetized atomic chain. The two spin excitations can propagate as individual, free magnons along the quantum magnet. But due to the ferromagnetic interaction between them, they can also stick together forming an elementary mobile magnetic domain with about the same probability.
Two technical achievements make it possible to both observe the bound state directly and to track its dynamical evolution. On the one hand the group has developed a method of imaging individual atoms on their individual lattice sites. With a special kind of a microscope the scientists can distinguish atoms with a flipped spin from the unflipped ones. On the other hand, they can trigger precisely at which moment the particles start to move. This is done by lowering the lattice height, which enhances the magnetic interactions between the atoms. When the lattice height is raised again after a certain time interval, the magnetic interaction is turned off again and the spin orientation of the atoms is “frozen out”. By taking snapshots of the actual spin patterns for a series of different evolution times the propagation of the ferromagnetic excitations can be measured with high resolution in space and time.
“With this method we can unambiguously separate states with bound magnons from those with free excitations,” Dr. Christian Groß, project leader at the experiment, explains. “In the first case, the two adjacent flipped spins stay together on their walk along the quantum magnet. In the second, the free magnons show anti-bunching in their motion. This means, if one spin excitation has travelled three lattice sites to the right the other one has moved the same distance in the opposite direction.
Bound states usually don’t hold forever – this is as valid in the quantum world as it is in real life. “According to our observation the number of magnon pairs decreases for long observation times,” Dr. Takeshi Fukuhara points out. “One possible reason for this is that the fragile spin waves couple to some extent to thermal excitations. At present we are working on a model which will describe the decay of bound states both quantitatively and qualitatively.”
The observation of elementary quantum magnetic phenomena helps to understand fundamental magnetic processes in solid state crystals. But the investigation of the dynamics of spin waves in one-dimensional quantum magnets is also relevant for potential applications. For example, the transport of quantum information along a chain of qubits can be strongly influenced by the formation of bound two-magnon states. Olivia Meyer-Streng
Original publication:
Takeshi Fukuhara, Peter Schauß, Manuel Endres, Sebastian Hild, Marc Cheneau, Immanuel Bloch, and Christian Groß
Microscopic observation of magnon bound states and their dynamics,
Nature, AOP 25 September 2013, DOI: 10.1038/nature12541