Reviewed by Lexie CornerJun 4 2024
A multinational research team led by Marcus Sperling, a START award project leader from the Faculty of Physics, University of Vienna, has stirred attention in the scientific community with groundbreaking discoveries in quantum physics. In their new study, the researchers reinterpret the Higgs process, which gives elementary particles mass and causes phase changes, using the idea of “magnetic quivers.” The results have recently been published in Physical Review Letters.
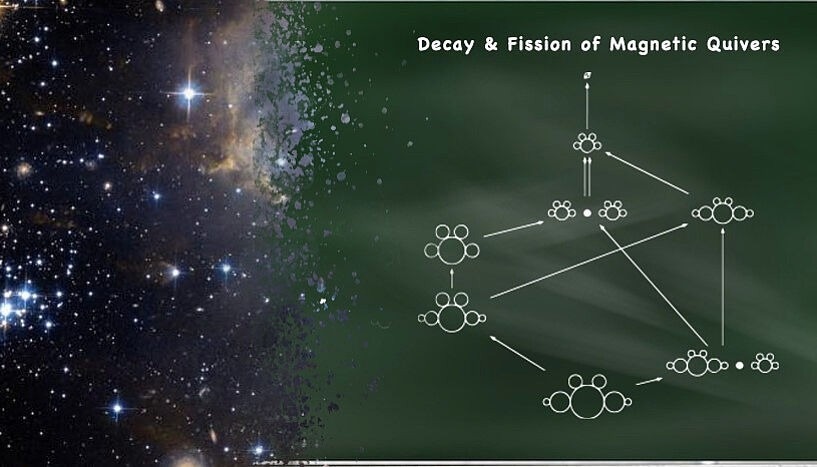The decay and fission of magnetic quivers provide insights into the physical and mathematical foundations of quantum field theories. QFTs are the framework for the description of countless physical phenomena, from subatomic particles to the universe. Image Credit: Pedro del Real
Marcus Sperling's study, which combines physics and mathematics, is based on Quantum Field Theory (QFT), a physical-mathematical notion within quantum physics that describes particles and their interactions at the subatomic level. He and colleagues have been developing the so-called “magnetic quivers” since 2018, a graphical tool that summarizes all the information required to create a QFT, presenting complicated interactions between particle fields or other physical variables plainly and intuitively.
Metaphorical Magnetic Quivers
A quiver is made up of directed arrows and nodes. The arrows indicate quantum fields (matter fields), and the nodes reflect the interactions between the fields, which can be strong, weak, or electromagnetic. The direction of the arrows depicts how the fields are charged during the interactions, such as the electric charge carried by the particles.
The term 'magnetic' is also used metaphorically here to point to the unexpected quantum properties that are made visible by these representations. Similar to the spin of an electron, which can be detected through a magnetic field, magnetic quivers reveal certain properties or structures in the QFTs that may not be obvious at first glance.
Marcus Sperling, Physicist, Universität Wien
Thus, they provide a realistic method for visualizing and analyzing complicated quantum phenomena, allowing fresh insights into the quantum world’s fundamental mechanics.
Supersymmetric QFTs
The current study investigated the stable ground states (vacua)—the lowest energy configuration in which no particles or excitations exist—in various "supersymmetric QFTs." These QFTs, with their reduced space-time symmetry, serve as a laboratory setting because they mirror genuine physical systems of subatomic particles while possessing mathematical features that assist calculations.
Sperling, an FWF START award winner, stated, “Our research deals with the fundamentals of our understanding of physics. Only after we have understood the QFTs in our laboratory environment can we apply these insights to more realistic QFT models.”
The notion of magnetic quivers, which is one of the key study subjects of Sperling’s START project at the University of Vienna, was utilized to offer a precise geometric description of the new quantum vacua.
Decay and Fission: Higgs Mechanism Reinterpreted
Antoine Bourget (University Paris Saclay), Marcus Sperling, and Zhenghao Zhong (Oxford University) used linear algebra calculations to show that, like radioactivity in atomic nuclei, a magnetic quiver can decay into a more stable state or fission into two separate quivers. These changes provide a novel understanding of the Higgs process in QFTs, which either decay into simpler QFTs or split into distinct, independent QFTs.
Sperling stated, “The Higgs mechanism explains how elementary particles acquire their mass by interacting with the Higgs field, which permeates the entire universe. Particles interact with this field as they move through space—similar to a swimmer moving through water.”
A particle with no mass often travels at the speed of light. However, when it interacts with the Higgs field, it “sticks” to it and becomes sluggish, resulting in the appearance of mass. As a result, to understand the universe’s fundamental building blocks and forces, a comprehension of the Higgs mechanism is required.
The “decay and fission” method is mathematically sound. It clearly explains stability and linear algebra concepts. It functions alone and requires no external inputs.
The results obtained using physics-inspired approaches apply not just to physics but also to mathematical research: they provide a basic and universally true explanation of the intricate, interconnected structures of quantum vacua, signifying a substantial breakthrough in mathematics.
Journal Reference:
Bourget, A., et al. (2024) Decay and Fission of Magnetic Quivers. Physical Review Letters. doi:10.1103/physrevlett.132.221603