The advent of the quantum age will transform the way the world operates. However, not all prospective applications for quantum computing are immediately beneficial. Asymmetric cryptosystems, which are based on the factoring of huge numbers, are best solved on quantum computers, which are uniquely adapted for this task, but the ramifications for cybersecurity are significant.
Image Credit: Anatolii Stoiko/Shutterstock.com
The current cybersecurity infrastructure must be replaced with a new, quantum-safe one in order to counteract the threat posed by the quantum computer. Cybersecurity developers are developing a number of technologies to accomplish this goal.
Quantum Key Distribution (QKD)
Quantum key distribution (QKD) is a ground-breaking approach that takes advantage of one of the cornerstones of quantum mechanics to transfer data securely over networks. Quantum nature, i.e., the observation of a state causes decoherence, is used advantageously in QKD. This guarantees the secrecy of encryption keys across an optical network. QKD prevents the interception of data, and any attempt to eavesdrop on the network will be noticed.
Vernam theorem dictates that any message consisting of binary symbols can be converted into a secret coded form if a secret key of the same length is used. A key can be a sequence of binary digits. The message is encoded by including the key with the message. Then, the receiver can only decode the message if the secret key is accessible. The success of such transmission relies on the secret key being used only once. This protocol describes how classical cryptography works. The task of QKD is to distribute the secret key between two quantum systems.
Traditionally, the sender-receiver pair between whom the quantum communication is conducted is called Alice and Bob, as shown in Figure 1. A third person, the eavesdropper who might intercept the message, is illustrated as Eve.
Protocols for QKD
Several mathematical protocols have been proposed for secure QKD. These are:
- BB84 protocol - Proposed by Charles Bennett and Gilles Brassard in 1984
- E91 protocol - Devised by Artur Ekert in 1991
- B92 protocol - Proposed again by Charles Bennett
- Continuous-variable B92 protocol - A variation of the B92
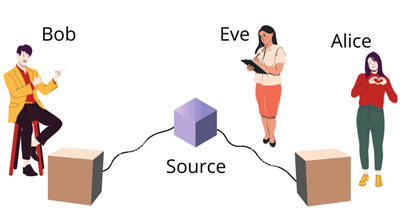
Figure 1: QKD scheme illustrating Alice, Bob, and Eve on a quantum network.
All these theoretical models use a physical device platform to generate entangled pairs of photons that are then sent from Alice to Bob. The algorithm ensures that a sequence of logical steps prevents Eve from intercepting the message.
The goal of the BB84 protocol is to completely encrypt the secret key into each individual photon's polarization state. Here, the photons are used for entanglement. The information encoded will be 'fragile' and unavailable to the eavesdropper because it is impossible to measure the polarization state of a single photon without also annihilating that photon. The photon must be detected by the listener, Eve in this case, at which point she must either expose herself or deliver an erroneous message.
The mathematical models of the devices, in particular, are also the foundation for the security of QKD. Therefore, it is crucial that they behave as expected while the protocol is being executed.
Device-Independent Quantum Key Distribution (DIQKD)
The device-independent quantum key distribution system (DIQKD) is a variation of QKD. It was first proposed by Mayers and Yao from Princeton University in 1998. DIQKD uses a Bell test to guarantee the correct and secure operation of the underlying devices.
DIQKD is tested on the E91 protocol. The basic idea of the E91 protocol is that if the so-called Clauser–Horne–Shimony–Holt (CHSH) value is greater than the classical value of 2, then the state shared by Alice and Bob is entangled. The CHSH inequality is often used in the proof of Bell's theorem. Satisfying the CHSH condition raises the potential for generating a secret key. Importantly, a conclusive inference can be drawn even without the knowledge of what measurements the devices are performing or in what exact dimensions. This leads to the notion of DIQKD, where assumptions of device behavior can be made independent of the measurements. DIQKD is naturally robust against implementation flaws because it negates the need to characterize the devices.
Implementing DIQKD
The challenge facing DIQKD is the key rate and noise tolerance of the protocol. A system that distributes high-quality entangled states with high detection effectiveness between two remote locations is necessary to execute DIQKD. To produce secret keys, the system must have a low quantum bit error rate (QBER) while exhibiting a strong Bell violation.
An implementation of DIQKD has been shown using Rubidium atoms (87RB) as the entanglement source. Two 87Rb atoms trapped and controlled separately in structures that are 400 m away and connected by a 700 m long fiber constituted the network channel. Zeeman split sub-energy levels on the ground state of 87Rb were used to encode the qubits. An entanglement swapping mechanism is used to entangle the two separated atoms. The system demonstrated a positive secret key rate of 0.07 bits in a fully device-independent configuration thanks to significant improvements in the noise tolerance and entanglement rate.
Outlook
DIQKD has been demonstrated to be a significant advancement toward an ultimate secure quantum communication network. Cutting-edge quantum connections are able to produce secret keys. Additionally, future quantum networks might make use of this quantum advantage by sharing entanglement across their nodes, making DIQKD the industry standard for secure communications.
References and Further Reading
Zhang, W., van Leent, T., Redeker, K. et al. A device-independent quantum key distribution system for distant users. Nature 607, 687–691 (2022). https://doi.org/10.1038/s41586-022-04891-y
Schwonnek, R., Goh, K.T., Primaatmaja, I.W. et al. Device-independent quantum key distribution with random key basis. Nat Commun 12, 2880 (2021). https://doi.org/10.1038/s41467-021-23147-3
Wen-Zhao Liu, Yu-Zhe Zhang, Yi-Zheng Zhen, Ming-Han Li, Yang Liu, Jingyun Fan, Feihu Xu, Qiang Zhang, and Jian-Wei Pan. Toward a Photonic Demonstration of Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 129, 050502 – Published 27 July 2022. https://link.aps.org/doi/10.1103/PhysRevLett.129.050502
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.