Neural-Network Quantum States to Approximate the Implicit Midpoint Rule Method

By Skyla BailyJan 28 2022

The curse of dimensionality is a significant obstacle in simulating highly interactive many-body quantum systems on classical computers. On closer inspection, however, the manifold physical quantum many-body states cover an increasingly limited region in Hilbert space. The next task is to find a variational ansatz with low degrees of freedom while accurately expressing physical situations.

Study: Real time evolution with neural-network quantum states. Image Credit: local_doctor/Shutterstock.com

This is explored in the journal Quantum. 

Following the recent success of artificial neural network techniques, there has been a lot of interest in extending them to quantum many-body systems, especially as an alternative to the wavefunction of (highly correlated) quantum systems.

The main feature of such neural network quantum states is to represent systems with chiral topological phases or to handle significant entanglement. In the context of real-time evolution, this could be a significant advantage over existing tensor network methods, as increasing entanglement with time requires an exponential increase in virtual bond dimensions, which limits the applicability of tensor network techniques to relatively short time intervals.

While the advantages of neural-network quantum states have been studied theoretically, empirical demonstrations of their feasibility for quantum time evolution are still rare. The time step vector is projected onto the tangent space of the variational manifold using the canonical Dirac-Frenkel time-dependent variational principle.

The Dirac-Frenkel principle is combined with Monte Carlo sampling in time-dependent variational Monte Carlo (tdVMC), which makes use of the locality of typical quantum Hamiltonians. This implies using the (pseudo-)inverse of a covariance matrix to follow the evolution of variational parameters over time.

Moreover, researchers find that in reality, tdVMC might be very sensitive to the pseudo-inverse cutoff tolerance used, or that “deep” neural-network quantum states need a prohibitively tiny time step. Researchers propose and investigate an alternate way for directly approximating a time step in a traditional ordinary differential equation (ODE) method by “training” the quantum state of the neural network at the following time step using (variations of) stochastic gradient descent.

Methodology

The objective is to solve the Schrodinger equation in a time-dependent manner. The Dirac-Frenkel variational concept is used in stochastic reconfiguration (SR). A novel technique that is more closely aligned with the neural network training paradigm is suggested. The researchers optimized the network parameters to minimize the error for each time step.

The implicit midpoint technique has two key advantages: first, it retains the symplectic form of Hamiltonian dynamics, and second, it avoids the need for intermediate values, which would make network optimization more difficult.

The Restricted Boltzmann Machine (RBM) is a neural-network design presented as a wavefunction ansatz. It has been proved to accurately reflect the ground state of numerous Hamiltonians. An RBM is made up of two layers of neurons, indicated as the “visible” and “hidden” layers, which are linked but have no intra-layer connections, as shown in Figure 1(a).

The error achieved with stochastic reconfiguration and the error acquired with this technique are compared in Figure 1(b). A pseudo-inverse threshold of 10^-10 was used to compute the time evolution labeled SR, whereas a threshold of 10^-9 was utilized for SR (2).

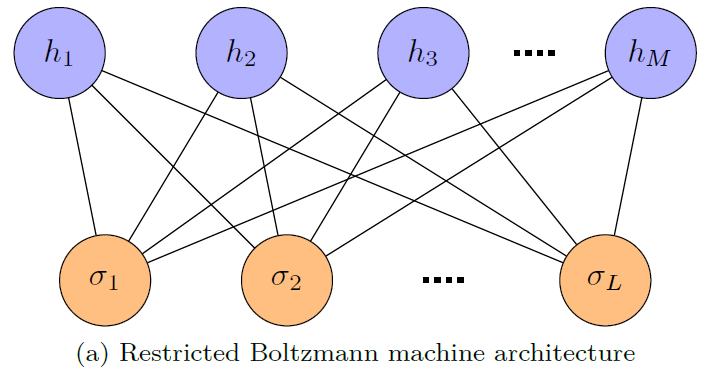
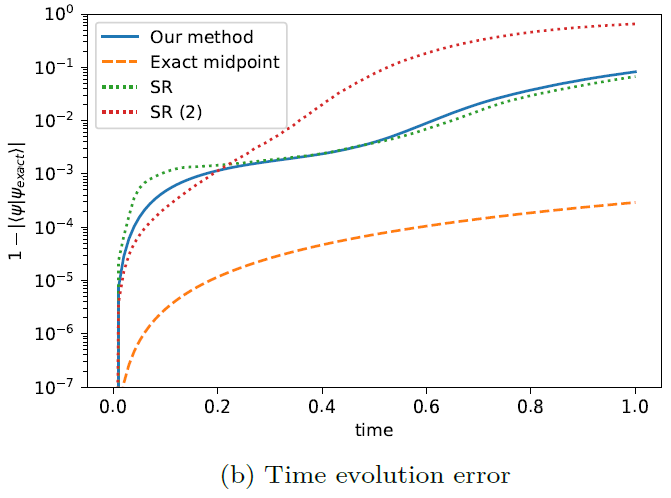
Figure 1 (a) Schematic diagram of a restricted Boltzmann machine showing the visible (orange) and hidden (blue) layers and the connections between the neurons. (b) Error in the time evolution performed using a RBM with 80 hidden units (1700 complex parameters in total), time step 0.01 and 50,000 uniformly drawn samples per time step. For comparison, SR and SR (2) show the stochastic reconfiguration method proposed by Carleo and Troyer, 2017, with two different pseudo-inverse thresholds. Image Credit: Gutiérrez, et al., 2022

The training was done on a single CPU with 64 GB of memory and 28 cores of multi-threading. The neural network architectures and optimization components of the method were written in customized C code, and the runs were scheduled and evaluated using a Python interface. A single optimization phase of the RBM network having 20 lattice sites and 50,000 samples takes around 3.6 seconds in this arrangement.

Results

To show the versatility of this technique, researchers modified the neural network architecture and study time evolution guided by the two-dimensional Ising model on a L × L lattice consisting periodic boundary conditions, as illustrated in Figure 2, using the output of a convolutional neural network directly.

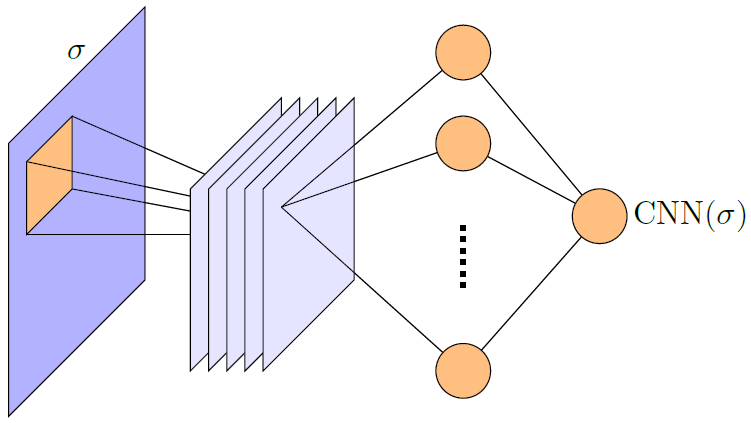
Figure 2. Schematic diagram of a convolutional neural network. Image Credit: Gutiérrez, et al., 2022

The overlap error concerning the specific wavefunction as a function of time is shown in the top row of Figure 3, as well as the error arising from a plain midpoint integration. Each time step was optimized with the same learning rate and iterations; however, a more careful optimization might reduce the error even further. The evolution of transverse magnetization is depicted in the bottom row of Figure 3 using our CNN ansatz and a numerically precise curve as a reference.

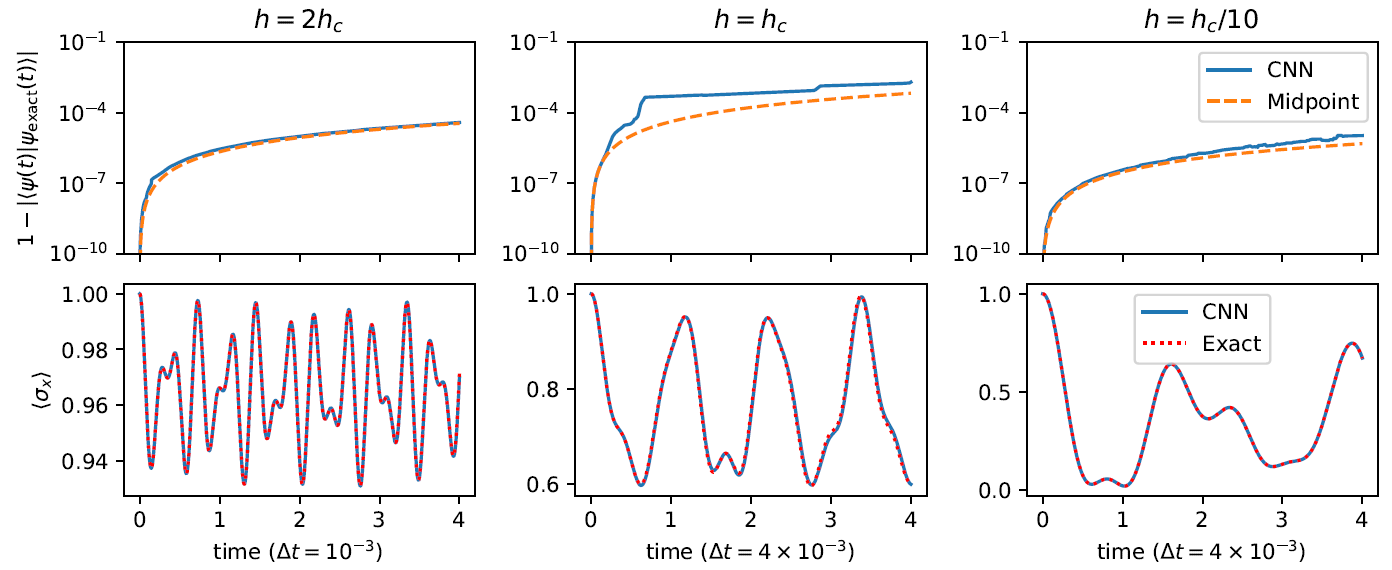
Figure 3. Overlap error (top row) and transverse magnetization (bottom row) of the real time evolution governed by the Ising Hamiltonian (Hochbruck and Lubich, 1998) on a 3 × 3 lattice after a quench of h. Each column corresponds to a different value of h after the quench, starting from “infinite” h. The researchers used 500 uniformly drawn samples for each individual optimization step of our method (CNN). Image Credit: Gutiérrez, et al., 2022

Conclusion

Researchers have shown that known neural network optimization approaches may be used to model the real-time evolution of quantum wavefunctions. Another advantage of this technique over SR is that it allows the neural network design to be altered on the fly, which might be important for capturing the system’s increasing complexity over time.

Using advanced machine learning approaches, such as deeper network designs with batch normalization and residual blocks, might enhance the findings shown here even more. The network parameters were optimized without any constraints in this study, however introducing symmetries or a specific structure, particularly to the CNN filters, might speed up and enhance the optimization.

Journal Reference:

Gutiérrez, I. L., & Mendl, C. B. (2022) Real time evolution with neural-network quantum states. Quantum, 6, p.627. Available Online: https://quantum-journal.org/papers/q-2022-01-20-627/.

References and Further Reading

1. Schmitt, M & Heyl, M (2020) Quantum Many-Body Dynamics in Two Dimensions with Artificial Neural Networks. Physical Review Letters, 125 (10), p.100503. doi.org/10.1103/PhysRevLett.125.100503.
2. Luo, D., et al. (2020) Autoregressive Neural Network for Simulating Open Quantum Systems via a Probabilistic Formulation. Available at: https://arxiv.org/abs/2009.05580.
3. Kloss, B., et al. (2020) Studying dynamics in two-dimensional quantum lattices using tree tensor network states. SciPost Physics, 9 (5), p.070. doi.org/10.21468/SciPostPhys.9.5.070.
4. Luo, D., et al. (2021) Gauge Invariant Autoregressive Neural Networks for Quantum Lattice Models. Available at: https://arxiv.org/abs/2101.07243.
5. Verdel, R., et al. (2021) Variational classical networks for dynamics in interacting quantum matter. Physical Review B, 103 (16), p.165103. doi.org/10.1103/PhysRevB.103.165103.
6. Hofmann, D., et al. (2021) Role of stochastic noise and generalization error in the time propagation of neural-network quantum states. Available at: https://arxiv.org/abs/2105.01054.
7. Fauseweh, B & Zhu, J-X (2020) Laser pulse driven control of charge and spin order in the two-dimensional Kondo lattice. Physical Review B, 102 (16), p165128. doi.org/10.1103/PhysRevB.102.165128.
8. Lee, C.-K., et al. (2021) A Neural-Network Variational Quantum Algorithm for Many-Body Dynamics. Physical Review Research, 3(2), p.023095. doi.org/10.1103/PhysRevResearch.3.023095.
9. Guo, C & Poletti, D (2021) Scheme for automatic differentiation of complex loss functions with applications in quantum physics. Physical Review E, 103 (1), p.013309. doi.org/10.1103/PhysRevE.103.013309.
10. Valenti, A., et al. (2021) Scalable Hamiltonian learning for large-scale out-of-equilibrium quantum dynamics.
11. De Nicola, S (2021) Importance sampling scheme for the stochastic simulation of quantum spin dynamics. SciPost Physics, 11 (3), p.048. doi.org/10.21468/SciPostPhys.11.3.048.
12. Vicentini, F., et al. (2021) NetKet 3: Machine Learning Toolbox for Many-Body Quantum Systems. Availabe at: https://arxiv.org/abs/2112.10526.
13. Meyerov, I., et al. (2020) Simulating quantum dynamics: Evolution of algorithms in the HPC context. Available at: https://arxiv.org/abs/2005.04681.
14. Orthodoxou, C., et al. (2021) High harmonic generation in two-dimensional Mott insulators. npj Quantum Materials, 6, p.76. doi.org/10.1038/s41535-021-00377-8.
15. Lin, S-H & Pollman, F (2021) Scaling of neural-network quantum states for time evolution. doi.org/10.1002/pssb.202100172.
16. Schmitt, M & Reh, M (2021) jVMC: Versatile and performant variational Monte Carlo leveraging automated differentiation and GPU acceleration. Available at: https://arxiv.org/abs/2108.03409.
17. Koch, R & Lado, L (2021) Neural network enhanced hybrid quantum many-body dynamical distributions. Physical Review Research, 3(3) p.033102. doi.org/10.1103/PhysRevResearch.3.033102.
18. Luo, D & Halverson, J (2021) Infinite Neural Network Quantum States. Quantum Physics. Available at: https://arxiv.org/abs/2112.00723.