This article provides an overview of harmonic motion, classical harmonic oscillators, and quantum harmonic oscillators.
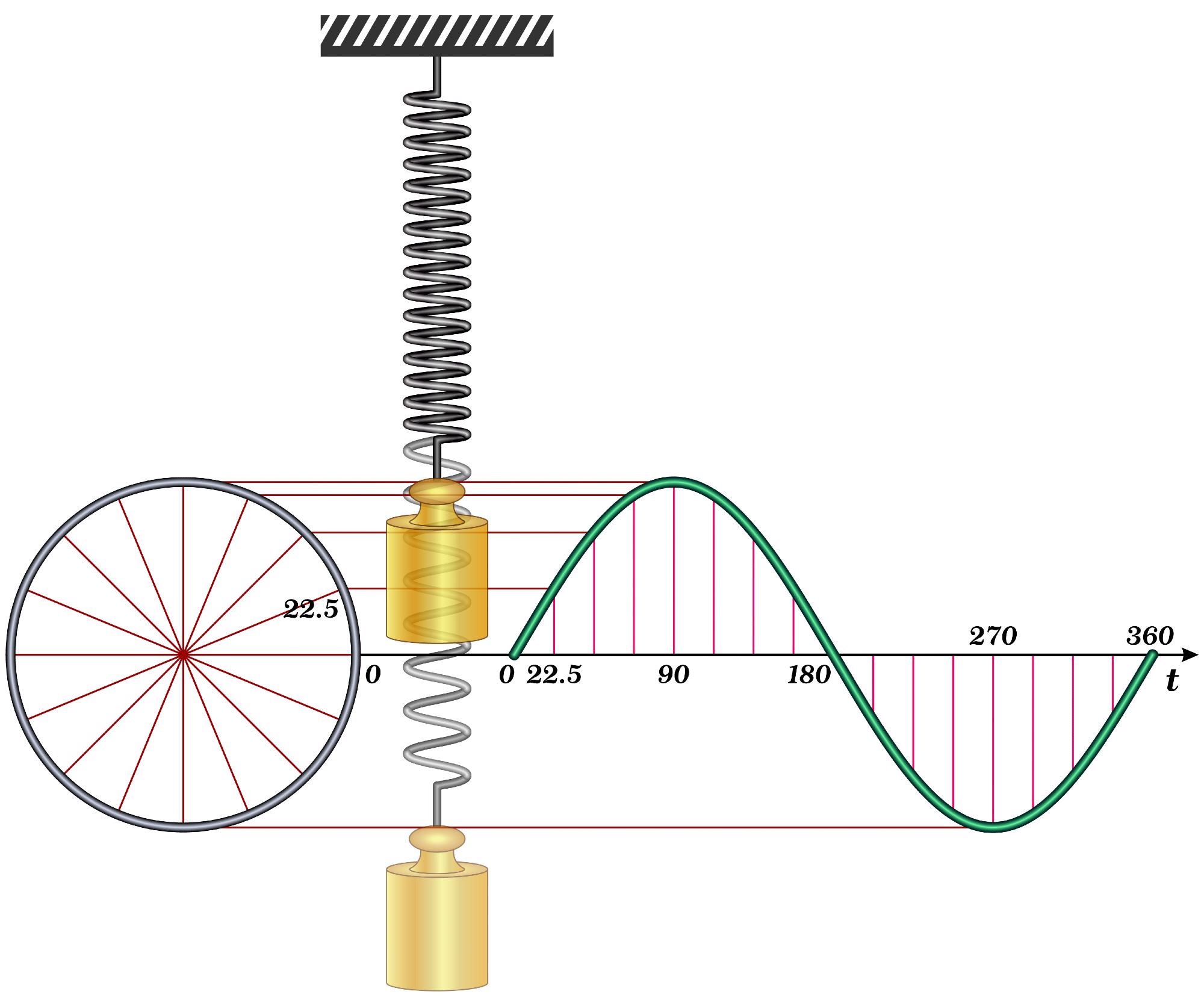
Image Credit: Fouad A. Saad/Shutterstock.com
What is Harmonic Motion?
Harmonic oscillators (HOs) are systems that exhibit and are often used to generate harmonic motion, which in most cases are simple harmonic motions (SHMs). SHM is a periodic motion with a sinusoidal time dependence in which the mass returns to its equilibrium position after a certain interval of time, and the acting force is opposed by the restoring force, which is proportional to the corresponding displacement and opposite in direction.
Some standard HOs are the mathematical models of spring, pendulum, elasticity, acoustic waves, electromagnetic waves, AC circuits, molecular vibration, lattice vibration, and several optical phenomena. Although in real-world applications a true harmonic motion is hindered by energy loss due to damping, the incorporation of periodic external energy is used to achieve the desired harmonic motion.
An SHM is mathematically represented by
x(t) = A.sin (ωt) + B.cos (ωt)
where x = displacement, ω = angular frequency, and t = time.
All HOs have a harmonic potential that drives oscillations, it is represented as a parabolic curve relative to the displacement. Based on the difference in mathematical approach between classical and quantum mechanics, HO is classified into classical oscillator (CO) and quantum oscillator (QO).
Classical Harmonic Oscillator
A spring-mass model is a typical example of CO in which macroscopic kinetics analysis is performed through classical mechanics. The acting force that stretches or compresses a spring is opposed by an equal restoring force due to its stiffness.
Fa = -Fr (‘-ve’ sign is due to opposite direction)
mẍ(t) = -kx(t)
mẍ(t) + kx(t) = 0
ẍ(t) + ω2x(t) = 0 (ω2 = k/m)
where Fa = acting force, Fr = restoring force, m = mass, k = stiffness, ẍ(t) = acceleration, and x(t) = displacement.
The maximum potential energy of the spring-mass model is V(x) = ½ kx2 or ½ mω2x2.
Quantum Harmonic Oscillator
Similarly, for QOs such as electromagnetic wave oscillators, linear transform eigenvector-eigenvalue-based Schrödinger equation is used. It has a Hamilton energy operator, the summation of the kinetic energy and potential energy as eigenvector and total energy as eigenvalues. Further, it is classified into two types, viz. time-dependent Schrödinger equation and time-independent Schrödinger equation, which is expressed as
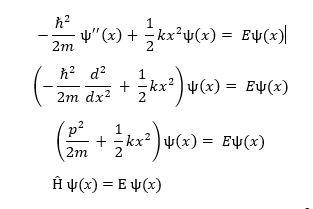
where ℏ = reduced Planck constant, p = momentum operator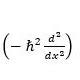 
, ѱ = wave function, E = total energy, and Ĥ = Hamiltonian energy operator.
The ground state energy of the QO model is E0 = ℏω/2, where the wavefunction is Gaussian and the subsequent eigenvalues are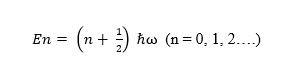 
The time-dependent Schrödinger equation is expressed as:
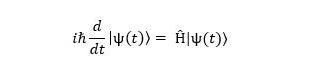
Importance of Schrödinger Equation in Quantum Harmonic Oscillators
Schrödinger equation has significant applications in quantum physics as harmonic motion is one of the fundamental motions in quantum mechanics and the equation gives the position (probability density) and momentum (continuity) of non-relativistic particles corresponding to their energy state.
Video Credit: TMP Chem/Youtube.com
Additionally, it applies to spinless particles, contrary to the Klein-Gordon equation and the Dirac equation. Moreover, the general form of the Schrödinger equation is true for quantum field theory (QFT), which is a combination of quantum mechanics and special relativity, also known as relativistic quantum mechanics.
However, the QO model with one particle, single SHM, or linear Schrödinger equation is of limited use in relativistic quantum mechanics due to the consideration of an uncertain number of particles. Moreover, there is a class of quantum oscillators, which is non-harmonic, non-linear, and the difference between each energy level is not constant (En+1 – En ≠ ℏω/2) such as Morse anharmonic oscillator.
Recent Studies on Harmonic Oscillators
Currently, many research works are focusing on the behavior of coupled quantum harmonic oscillators.
In a recent study, researchers developed a new methodology to precisely estimate the resonance frequency of a linear harmonic oscillator, which is fundamentally limited by the presence of noises owing to thermodynamic and quantum perturbations, by using the Cramer Rao lower bound model under a wide range of measurement conditions. Another study suggested that the upper bound of entanglement between identical oscillators is approximately inversely proportional to the particle number.
References and Further Reading
Lecture05.dvi (umich.edu)
https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_
https://www.bu.edu/quantum/notes/QuantumMechanics/HarmonicOscillator.pdf
Fundamental limits and optimal estimation of the resonance frequency of a linear harmonic oscillator | Communications Physics (nature.com)
Quantum entanglement in coupled harmonic oscillator systems: from micro to macro - IOPscience
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.